Mapping Environmental Justice in the Muhheakunnuk Valley

We’ll explore environmental justice in Dutchess County, within the Muhheakunnuk or Hudson Valley region.

Purpose

You will:

  • Load tabular and spatial data in R.

  • Plot data using ggplot geoms.

  • Use a spatial join to attach Toxic Release Inventory (TRI) facilities to neighborhoods (tracts).

  • Create a simple exposure indicator. Compute:

    • TRI facilities per tract
    • TRI per square mile

  • Explore associations between TRI facility locations and neighborhood indicators such as asthma prevalence, unemployment, and the percentage of children in a neighborhood.

  • Create choropleth maps of Dutchess County, NY using ggplot.

Install packages

  • You only need to do this step once.
install.packages("sf")) #popular package for working with spatial data

Load the required packages

library(tidyverse)
library(sf)

First, let’s use the read_sf function from the sf package to read in spatial data…

Step 1: Load spatial data

We will work with two spatial datasets:

  • dutchess_indicators: Census tracts with demographic and socioeconomic indicators.

  • tri_facilities: TRI facilities (point locations).

# County variables (e.g., median household income)
#dutchess_indicators <- read_sf("data/dutchess_indicators.geojson")

# Point locations of TRI facilities for the Hudson Valley
#tri_facilities <- read_sf("data/toxic_release_inventory_epa.shp")

# Make sure that both layers are projected on the earths surface 
# correctly: they need to have the same projection
tri_facilities <- st_transform(tri_facilities, 
                               st_crs(dutchess_indicators))

Explore exposure to pollutants from toxic release facilities

Explore and compare the location of the U.S. Environmental Protection Agency’s list of facility location producing or working with toxic chemicals.

  • tri_facilities contains one row for each Toxic Release Inventory (TRI) facility in the Hudson Valley. We will work with those in Dutchess County, NY.

Dutchess County, NY Federal Data

For this activity we’ll use the Census Tract geography, which are roughly neighborhood-sized areal units.

Each observation represents a Census Tract “neighborhood” and contains various social, economic, and built environment attributes for that neighborhood.

Our data

dutchess_indicators includes:

  • Join identifier for each Census Tract: join_ID

  • Total population: tot_pop

  • Area in square miles: area_sqmiles

  • Median Household Income: median_hh_income

  • Asthma prevalence among adults: asthma_rate

Each row in tri_facilities represents the registration of a site that emits toxic material into the land, air, or water.

Display the names of the variables in the dutchess_indicators dataset.

glimpse(dutchess_indicators)

Step 2: Get to know the data


Explore the variables

Create ggplot charts to summarize the data.


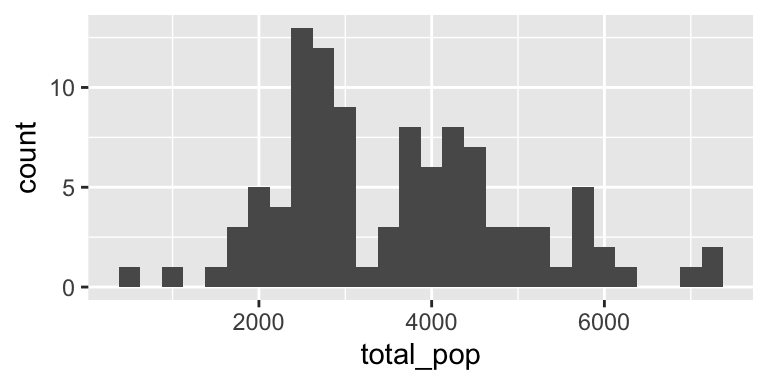
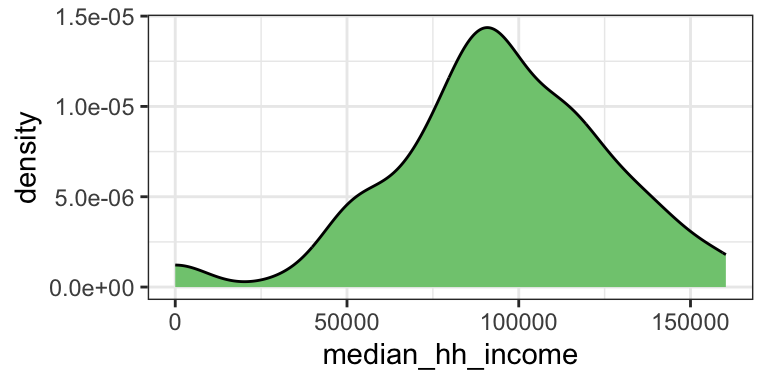
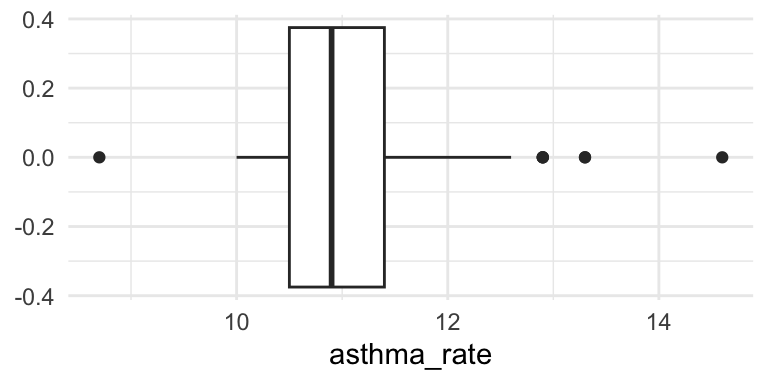
First, let’s explore the numerical distribution of some of our numerical variables…

Numerical distribution

Histogram

#Total population:  Histogram
dutchess_indicators %>% 
  ggplot(aes(x = total_pop)) + 
  geom_histogram(binwidth = 250) # Specify the binwidth

Density plot

# Density plot
dutchess_indicators %>% 
  ggplot(aes(x = median_hh_income)) + 
  geom_density(fill="#7fc97f") +
  theme_bw() # Add a plot theme

Boxplot

# Box plot
dutchess_indicators %>% 
  ggplot(aes(x = asthma_rate)) + 
  geom_boxplot()  +
  theme_minimal()

Maps!

Map the point locations of TRI facilities

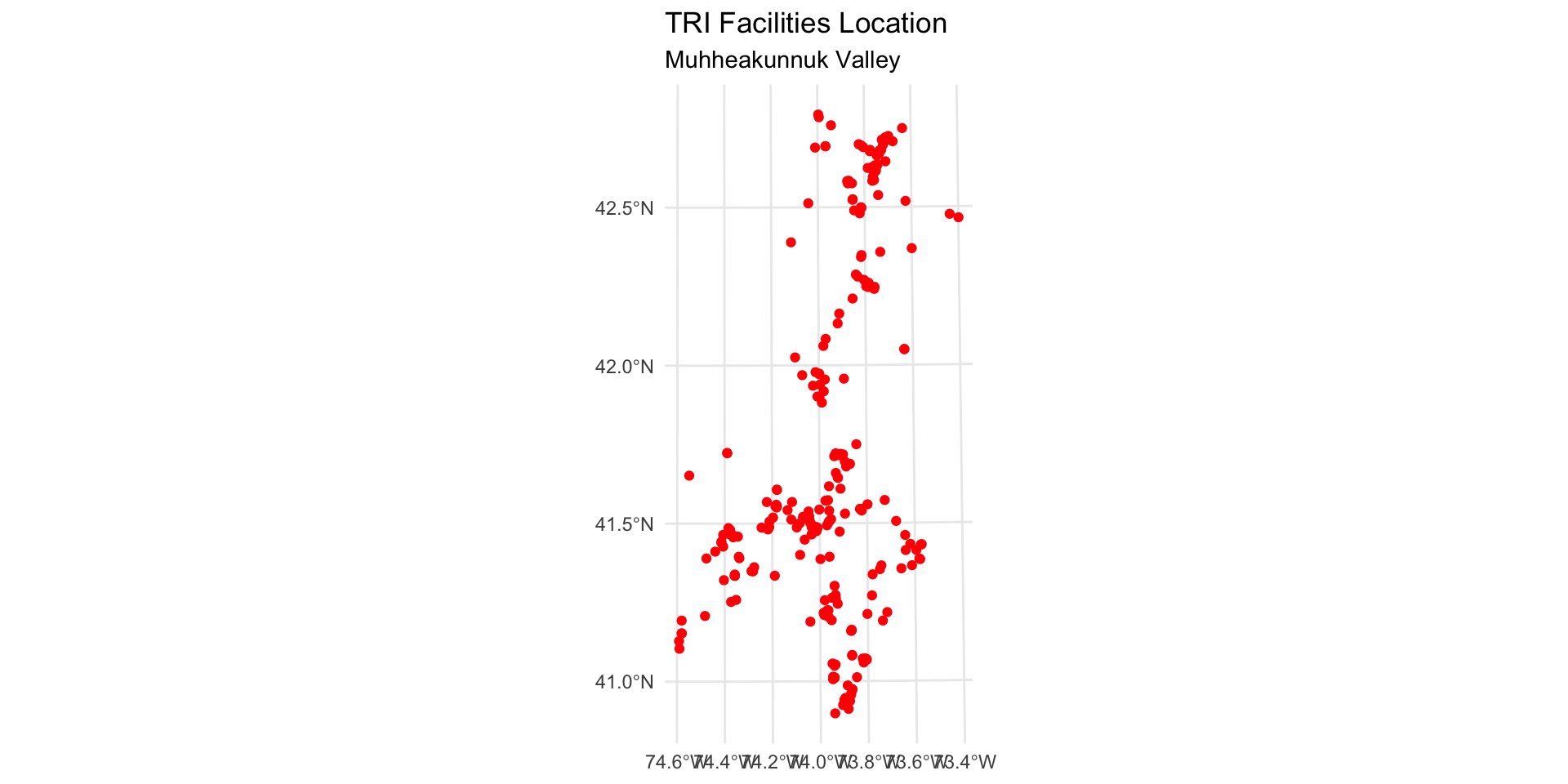
Map the point locations of TRI facilities

tri_facilities %>%
  ggplot() +
  geom_sf(color = "red") +
  labs(title="TRI Facilities Location", subtitle = "Muhheakunnuk Valley") +
  theme_minimal()

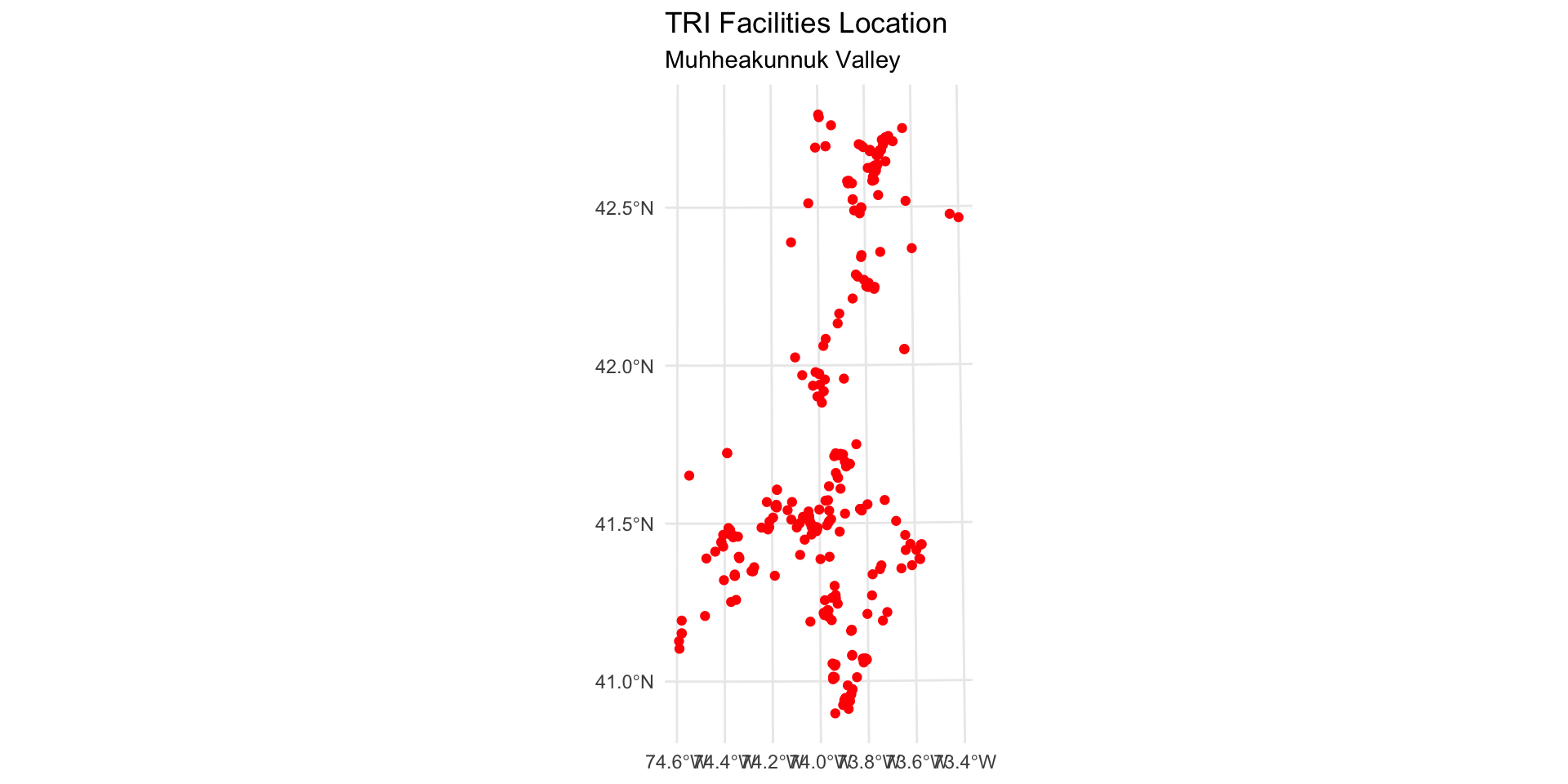
Map the point locations of TRI sites

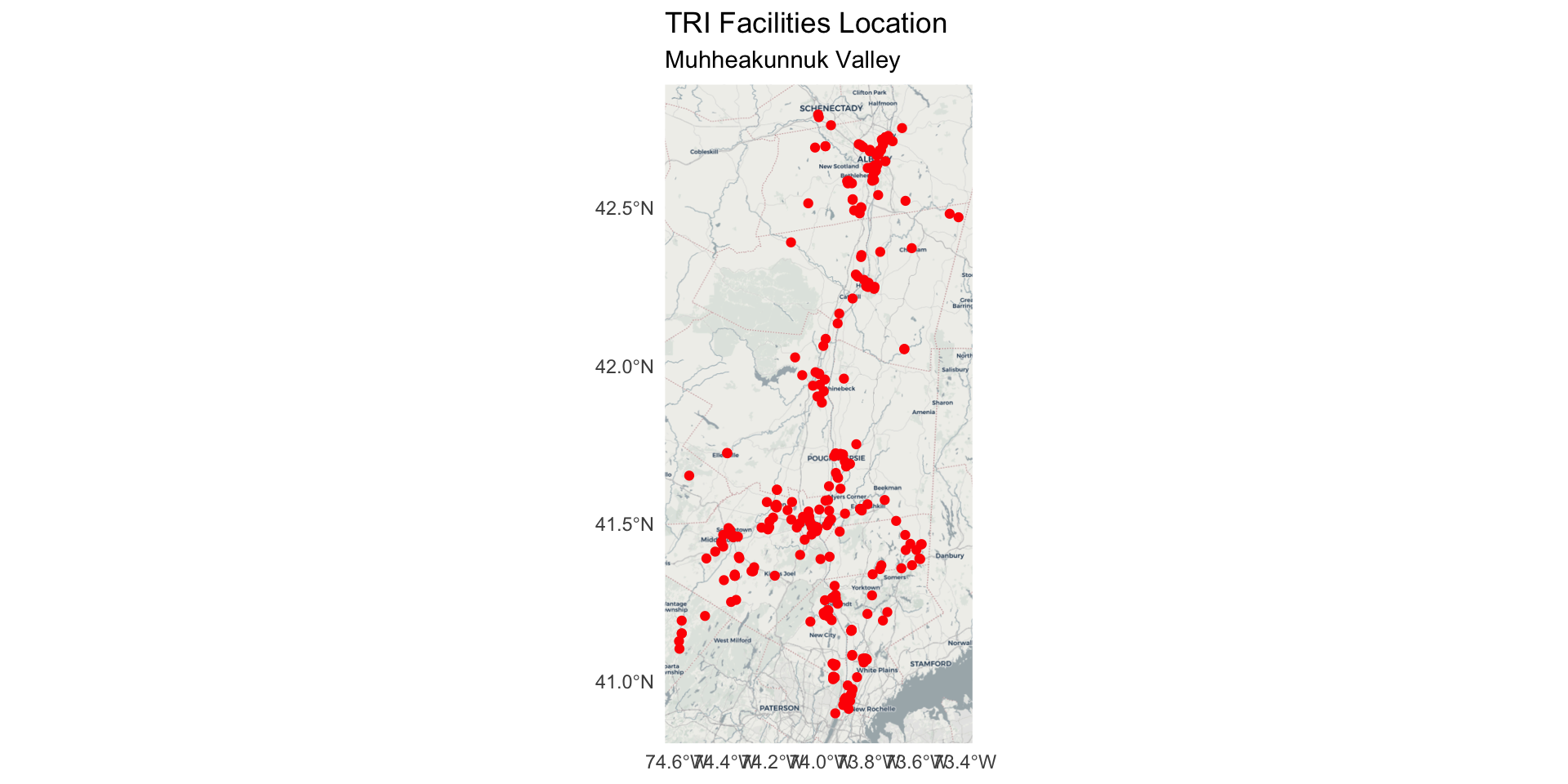
Map the point locations of TRI sites

This time, with a basemap.

  • Install and load the ggspatial library.

  • Set the zoom = argument to display a clear, readable base map underneath the geom_sf() point layers.

tri_facilities %>%
  ggplot() +
  annotation_map_tile(zoom = 9, type = "cartolight") + # add basemap (other type options include: "osm", "cartodark")
  geom_sf(color = "red") +
  labs(title="TRI Facilities Location", subtitle = "Muhheakunnuk Valley") +
  theme_minimal()

Spatial join

st_join() adds the columns from one spatial dataset to another based on how their shapes overlap or relate in space.

Use ?st_join to learn more.

Examples of spatial join relationships

  • One point falls inside a polygon

  • Two polygons touch each other

  • A line crosses a boundary

  • One feature is the nearest to another

Spatial join

  • It uses intersects, meaning if shapes touch or overlap, they get joined.

  • It does not require a matching column

  • It does not change the shapes

Imagine placing transparent paper maps on top of each other. Where features line up, st_join() copies the information from one map onto the other.

Spatial join

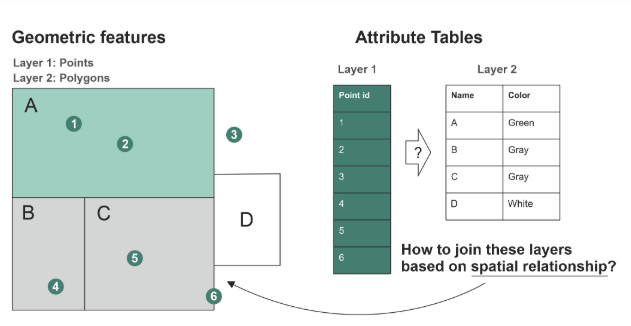
st_within and st_intersects argument inside st_join (Hint: use ?function_name to learn more.)

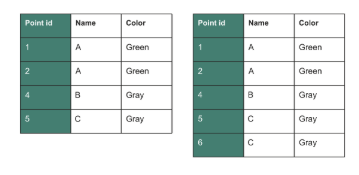
Summary of a spatial join

  • st_join() is a join by location, not by column.

  • It adds attributes from one spatial layer to another.

  • It uses spatial relationships like intersects, within, contains, or nearest.

  • Used for the task of transferring attributes across overlapping layers:

    • Assigning census data to point locations (e.g., TRI sites)

    • Matching point data attributes to neighborhoods

Use the same coordinate system

In order to conduct any spatial operations like st_join both layers need to be projected onto the earth surface in the same way.

  • We do this using a coordinate reference system or crs 
k12_points <- st_as_sf(k12_df, coords = c("x", "y"), 
                       crs = 4326) %>% # Always load new data using the default crs 4326
  st_transform(3626) # transform the coordinate reference system to be the same as dutchess_indicators and dutchess_tri 

# Alternative approach
k12_points <- st_as_sf(k12_df, coords = c("x", "y"), 
                       crs = 4326) %>% 
  st_transform(st_crs(dutchess_indicators))

Step 3: Spatial join

Purpose: We want to know which neighborhoods contain TRI facilities. So, we attach each tract join_ID to the TRI facilities observations.

  • It tells which neighborhood (aka census tract) each TRI observation is within.

  • We use st_join() with a st_within predicate to attach tract attributes to each TRI point.

tri_in_tracts <- st_join(tri_facilities, 
                         dutchess_indicators, 
                         join = st_within)

Next, we use the result of the st_join to create a table that tells us how many TRI facilities are within each neighborhood.

  • We us the unique join_ID to create a frequency table of TRI per tract.

  • Then, we normalize by creating a variable that holds TRI facility density: TRI per square mile.

Step 4: Counting TRI facilities per tract


Now we aggregate to the tract level: how many TRI facilities are located in each tract?

What function do we need to get the number of observations per neighborhood (tract)?

Step 4: Counting TRI facilities per tract


Now we aggregate to the tract level: how many TRI facilities are located in each tract?

tri_counts <- tri_in_tracts %>%
  st_drop_geometry() %>%
  count(join_ID, name = "tri_n")

Step 5: Join and compute TRI facilities per square mile


  • Join the TRI per neighborhood counts back with the full dataset using a left_join by the unique join key in each data set: join_ID

  • Create a new varialble tri_per_sqmile with TRI facilities per square mile.

  • Store the result in a new sf object dutchess_tri

dutchess_tri <- dutchess_indicators %>% 
  left_join(tri_counts, by="join_ID") %>% 
  mutate(tri_n=replace_na(tri_n,0), 
         tri_per_sqmile = tri_n /area_sqmiles)

Summary statistics

Running the summary on a data frame object gives you the min, max, 1st quartile, median, mean, 3rd quartile, and max for each numerical variable.

to_summary <- dutchess_tri %>% 
  select(where(is.numeric))
summary(to_summary)
   total_pop     area_sqmiles     median_hh_income percent_children
 Min.   : 536   Min.   : 0.1256   Min.   :     0   Min.   : 0.00   
 1st Qu.:2616   1st Qu.: 2.6370   1st Qu.: 78770   1st Qu.:15.20   
 Median :3502   Median : 5.5814   Median : 93278   Median :18.00   
 Mean   :3609   Mean   :11.0726   Mean   : 94374   Mean   :17.73   
 3rd Qu.:4522   3rd Qu.:14.3142   3rd Qu.:114663   3rd Qu.:21.50   
 Max.   :7137   Max.   :56.9210   Max.   :160294   Max.   :28.20   
 percent_white   percent_black   percent_latine  unemployment_rate
 Min.   :11.20   Min.   : 0.40   Min.   : 1.70   Min.   : 0.000   
 1st Qu.:64.40   1st Qu.: 2.70   1st Qu.: 7.90   1st Qu.: 2.300   
 Median :73.40   Median : 5.20   Median :11.50   Median : 4.200   
 Mean   :68.98   Mean   :10.28   Mean   :13.02   Mean   : 4.773   
 3rd Qu.:79.00   3rd Qu.:10.40   3rd Qu.:16.90   3rd Qu.: 6.850   
 Max.   :89.50   Max.   :60.80   Max.   :30.90   Max.   :16.100   
  asthma_rate    low_food_access prox_traffic_pollution     tri_n       
 Min.   : 8.70   Min.   :   0    Min.   :   0.0         Min.   :0.0000  
 1st Qu.:10.50   1st Qu.:2055    1st Qu.:  23.2         1st Qu.:0.0000  
 Median :10.90   Median :2964    Median :  79.8         Median :0.0000  
 Mean   :11.09   Mean   :3034    Mean   : 183.9         Mean   :0.4369  
 3rd Qu.:11.40   3rd Qu.:4074    3rd Qu.: 200.0         3rd Qu.:0.0000  
 Max.   :14.60   Max.   :6245    Max.   :1719.9         Max.   :6.0000  
 tri_per_sqmile            geometry  
 Min.   :0.0000   POLYGON      :103  
 1st Qu.:0.0000   epsg:3626    :  0  
 Median :0.0000   +proj=tmer...:  0  
 Mean   :0.1665                      
 3rd Qu.:0.0000                      
 Max.   :2.2206

Step 6: Map TRI facilities per square mile

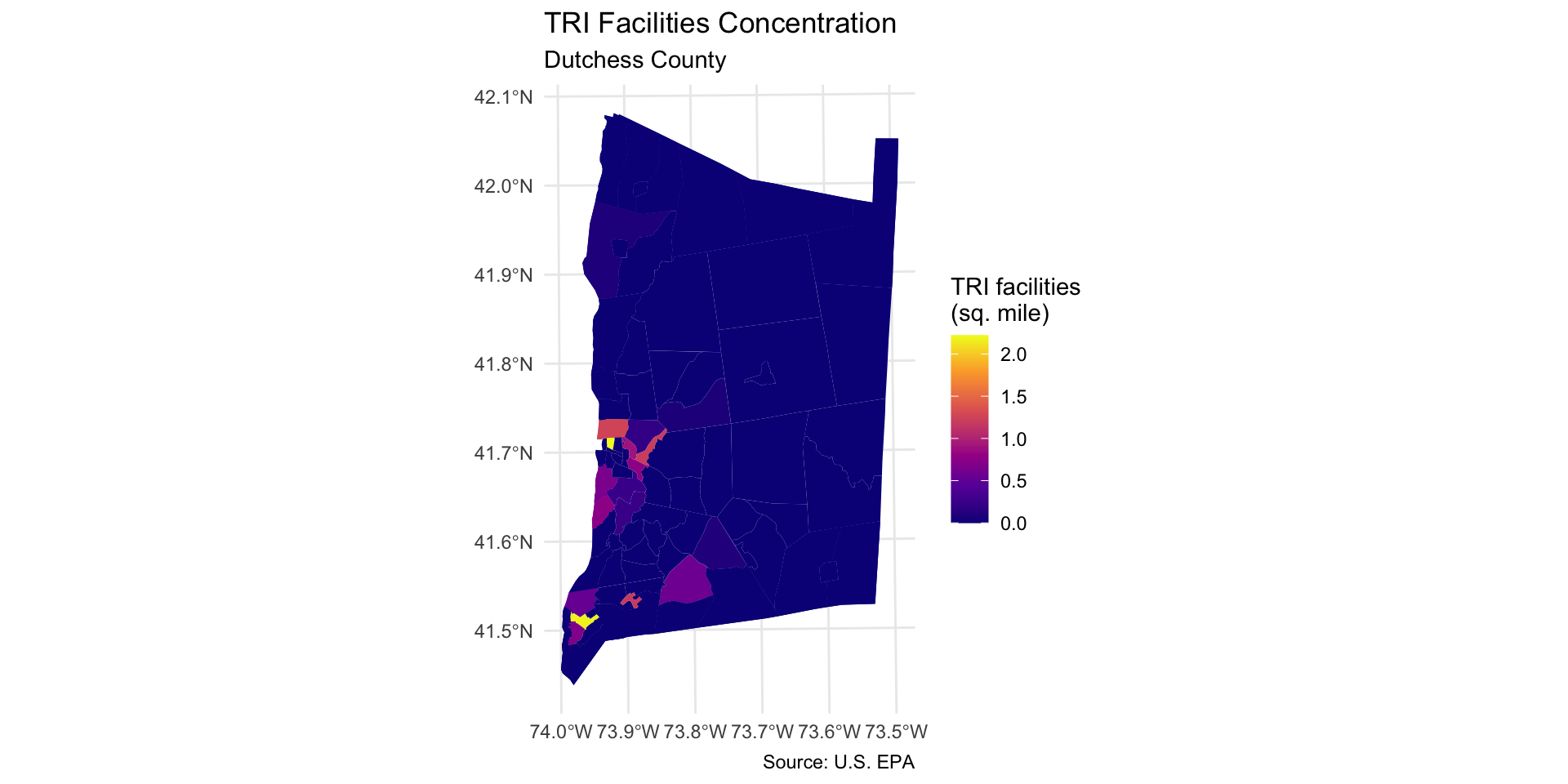
Step 6: Map TRI facilities per square mile


Map the count of TRI facilities per square mile across each neighborhood using geom_sf:

  • Use caption = "Source: U.S. EPA" to add a source note to the bottom of the map extent.
dutchess_tri %>%
  ggplot() +
  geom_sf(aes(fill = tri_per_sqmile), color = NA) +
  scale_fill_viridis_c(option="C", name="TRI facilities\n(per tract)") +
  labs(title="TRI Facilities Concentration", 
       subtitle="Dutchess County",
       caption = "Source: U.S. EPA")  +
  theme_minimal()

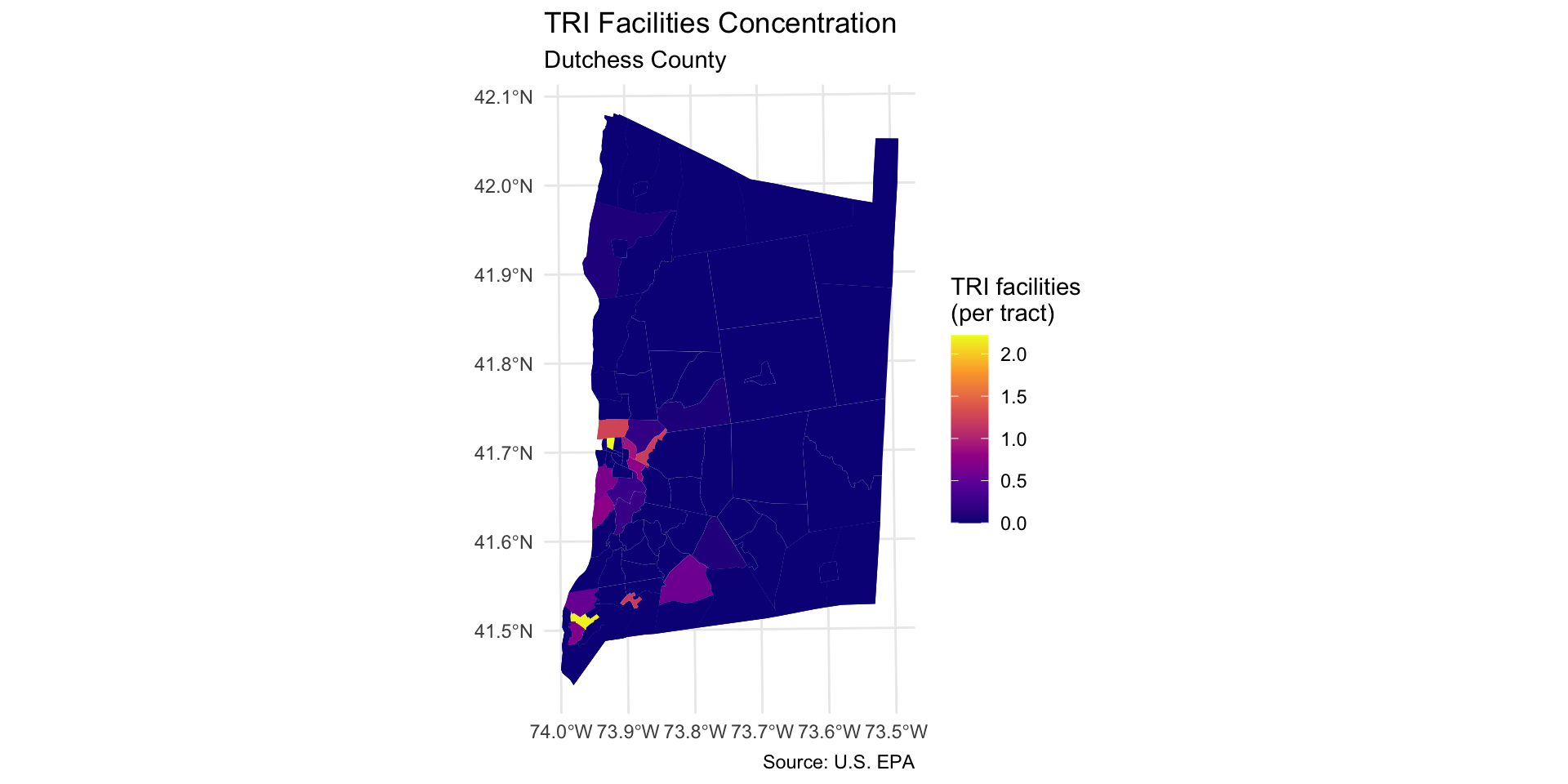
Step 7: Map other indicators of interest

Select another two or three variables from the dutchess_tri data frame to map. Change the fill = argument in the geom_sf() function to display the new indicator.

You will also need to change the fill legend title and title of the map.

dutchess_tri %>%
  ggplot() +
  geom_sf(aes(fill = asthma_rate), color = NA) +
  scale_fill_viridis_c(option="C", name="Asthma prevalence (%)") +
  labs(title="Asthma among adults", 
       subtitle="by Census Tract | Dutchess County",
       caption = "Source: U.S. CDC Places for Better Health") +
  theme_minimal()

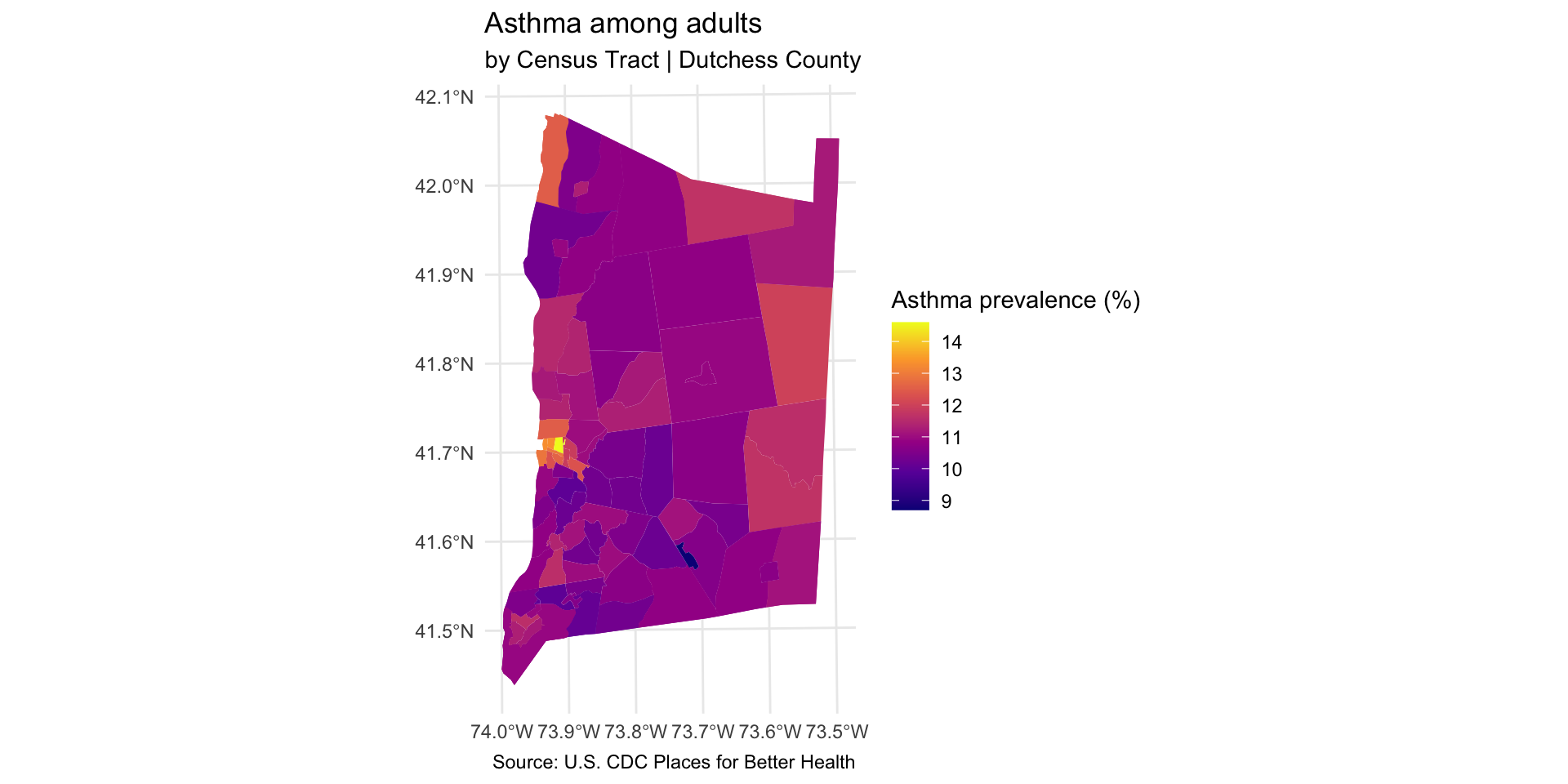
Step 8: Explore associations with neighborhood indicators


We can now explore how the location of TRI facilities is associated with neighborhood-level indicators.

Scatter plot to explore correlation

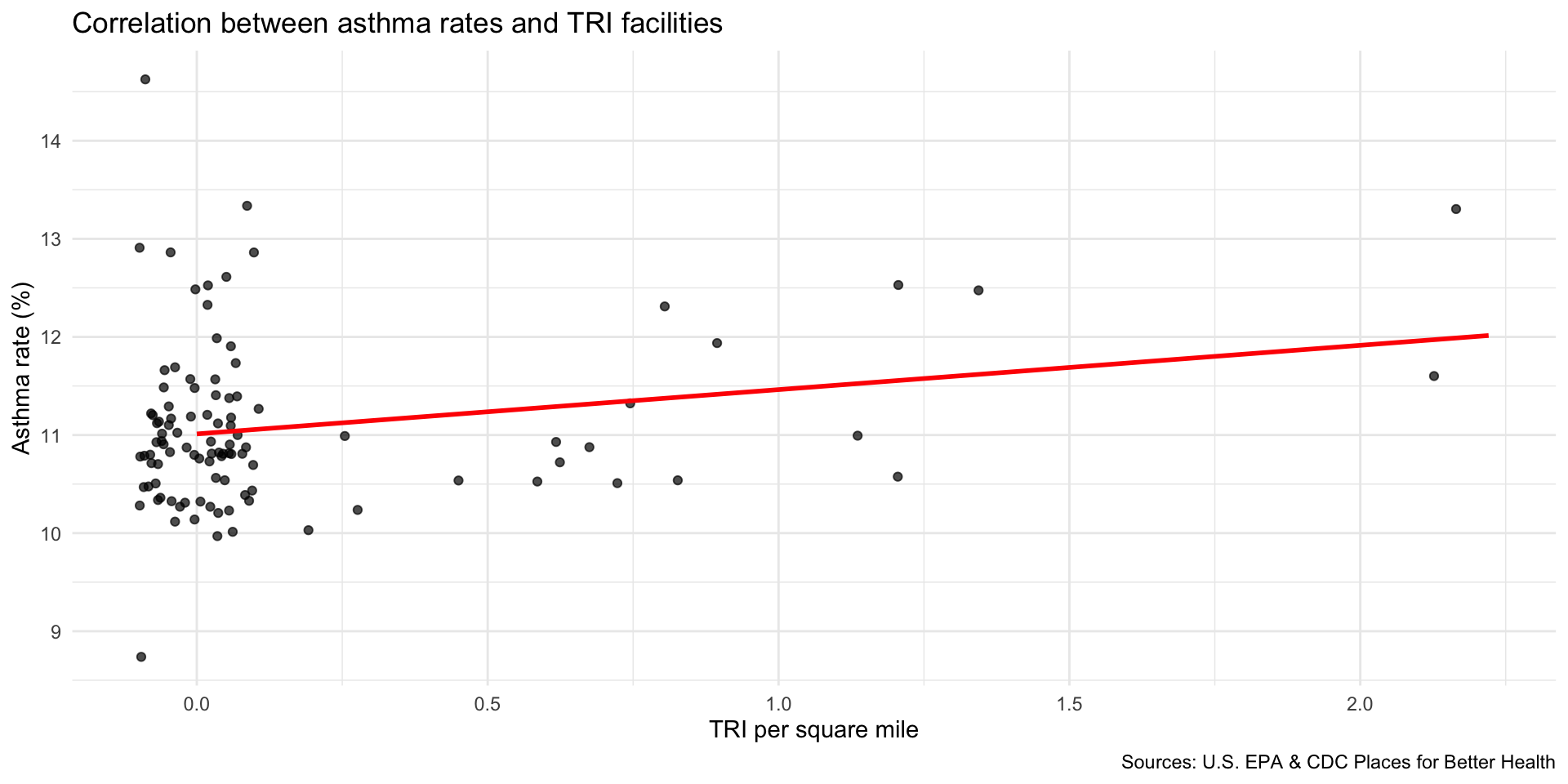
Compare TRI facilities tri_per_sqmile with the prevalence of asthma among the population: asthma_rate

Are neighborhoods with a higher concentration of TRI facilities near adults correlated with higher rates of asthma?

  • Use geom_smooth(method="lm") to add a linear regression line to your plot.

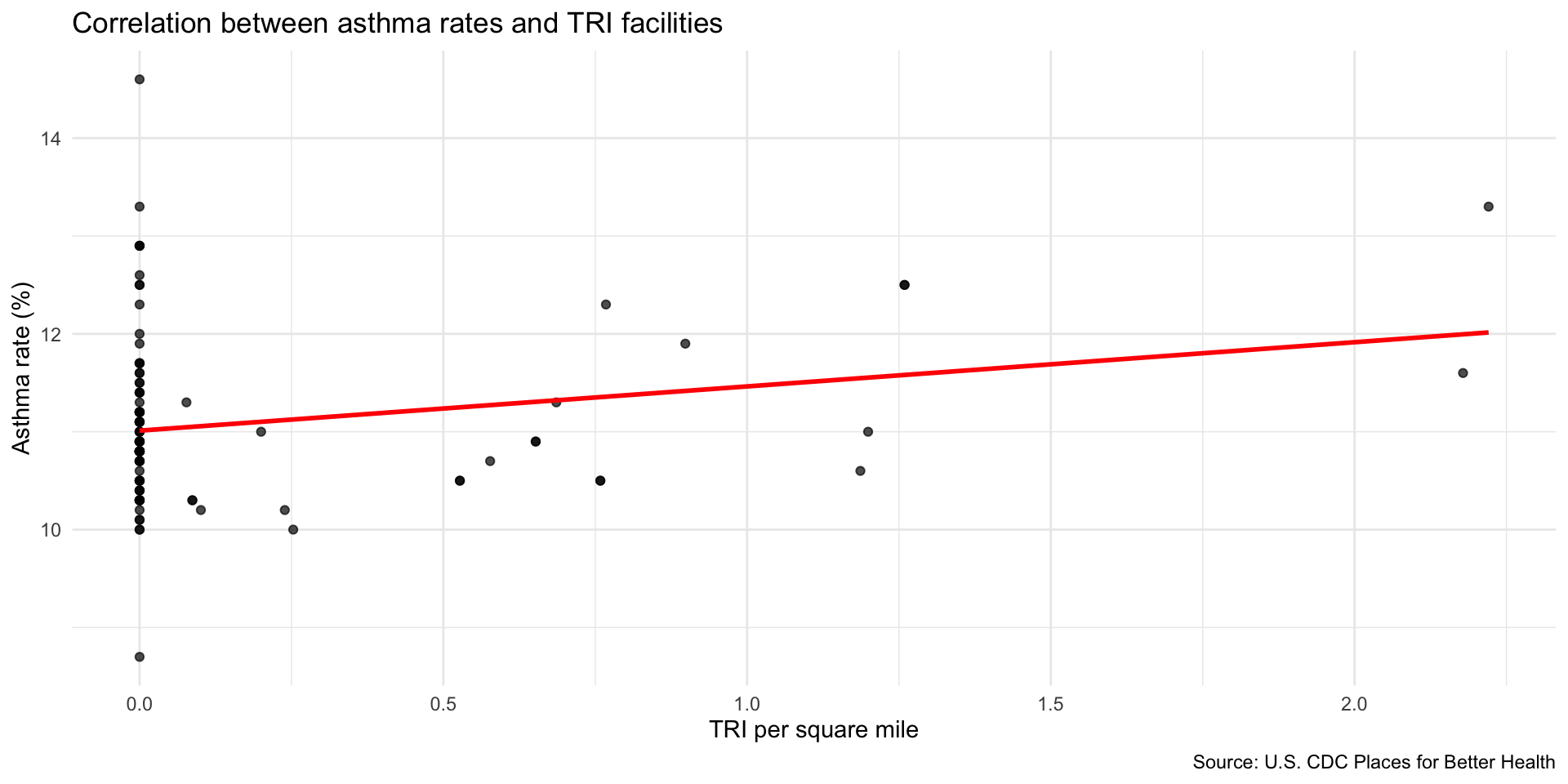
Use geom_jitter() to better observe the clustering of observations

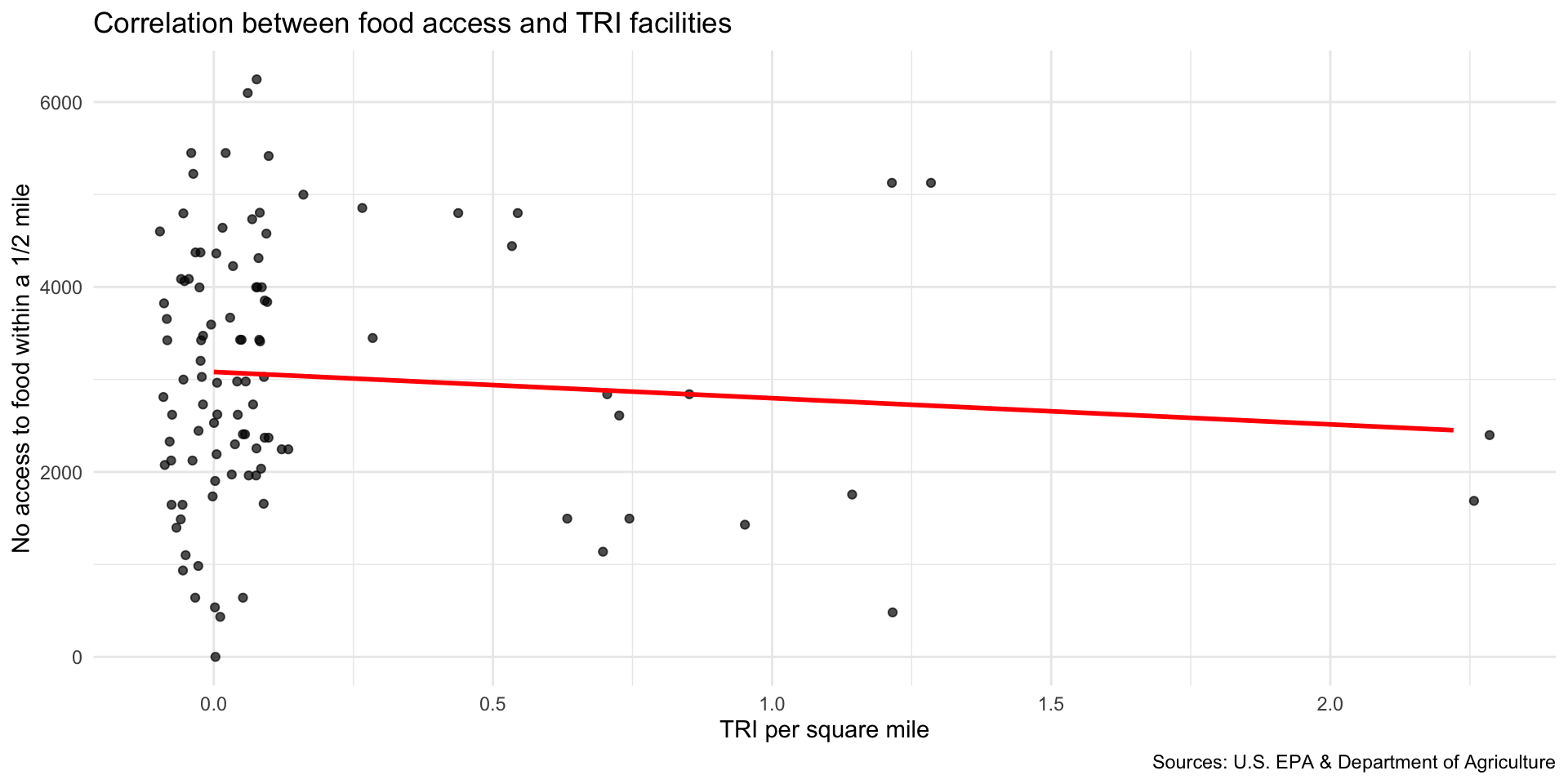
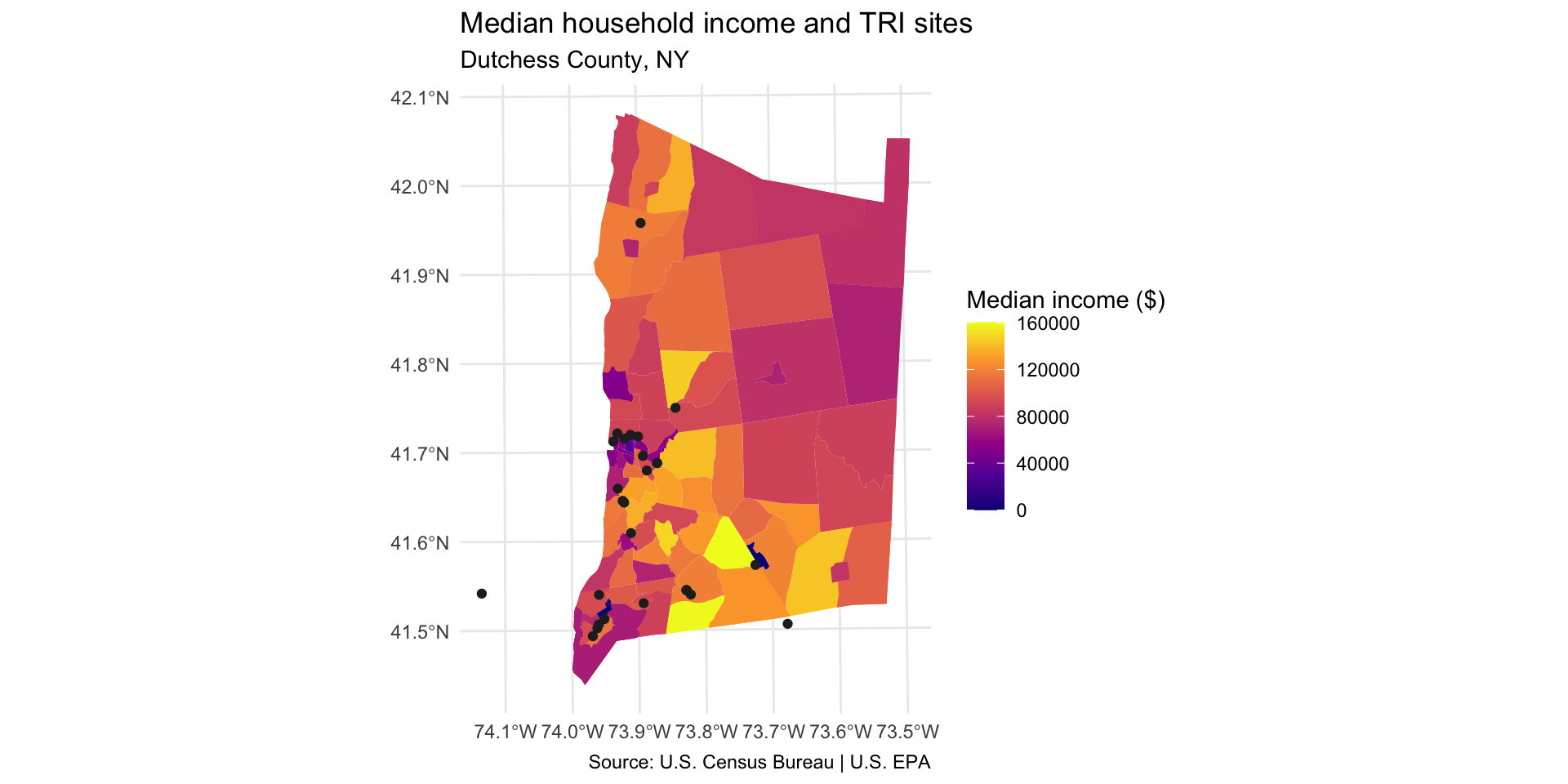
Step 9: Map TRI facility points with median household income

Compare TRI facility locations with the median household income in the neighborhood median_hh_income.

Step 9: Map TRI facility points with median household income

  • First, create a TRI layer that only includes facilities within Dutchess County.

    • Use the COUNTY_NAM variable to identify sites in Dutchess County.

    • Use distinct to identify how the Dutchess County entry is formatted in this dataset.

    • NOTE: there is at least one TRI facility that appears outside of Dutchess County due to errors in the EPA database.

Create a TRI layer that only includes facilities within Dutchess County

distinct(tri_facilities, COUNTY_NAM)
        COUNTY_NAM
1           ORANGE
2           ULSTER
3         COLUMBIA
4           GREENE
5         DUTCHESS
6    ORANGE COUNTY
7  COLUMBIA COUNTY
8    ULSTER COUNTY
9  SULLIVAN COUNTY
10   GREENE COUNTY
11 DUTCHESS COUNTY
12          PUTNAM
13     WESTCHESTER
14          ALBANY
15        ROCKLAND
16          BERGEN
17      RENSSELAER
18     SCHENECTADY
19          SUSSEX
20   ALBANY COUNTY
21   SUSSEX COUNTY
tri_dutchess <- tri_facilities %>% 
  filter(COUNTY_NAM == "DUTCHESS")

Make an interactive map with the tmap package

Install and load the tmap package.

#install.packages("tmap") 
library(tmap)

tmap_mode("view")  # set tmap to interactive map mode

tm_shape(tri_dutchess) +
  tm_symbols(col = "red", size = 0.2)

Note: you could use this interactive to identify the point(s) outside of Dutchess County (on the west of the estuary), then filter them out for the final map. For example, use `filter(REGISTRY_I != 110070690536)

Step 9: Map TRI facility points with median household income

  • In order to show two layers on the same ggplot map, you will need to use the data = argument inside your geom_sf. For example: geom_sf(data = sf_dataset).

  • Are neighborhoods with a higher concentration of TRI facilities more likely to have higher or lower median income?

  • Note: you will see that one TRI facility location showing up on the west side of estuary has an incorrect entry in the COUNTY_NAM variable. Ideally, we would remove this observation, but we can keep it in there for now.

dutchess_tri %>%
  ggplot() +
  geom_sf(aes(fill = median_hh_income), color = NA) +
  scale_fill_viridis_c(option="C", name="Median income ($)") +
  geom_sf(data = tri_dutchess) +
  labs(title="Median household income and TRI sites", 
       subtitle="Dutchess County, NY",
       caption = "Source: U.S. Census Bureau | U.S. EPA"
       ) +
  theme_minimal()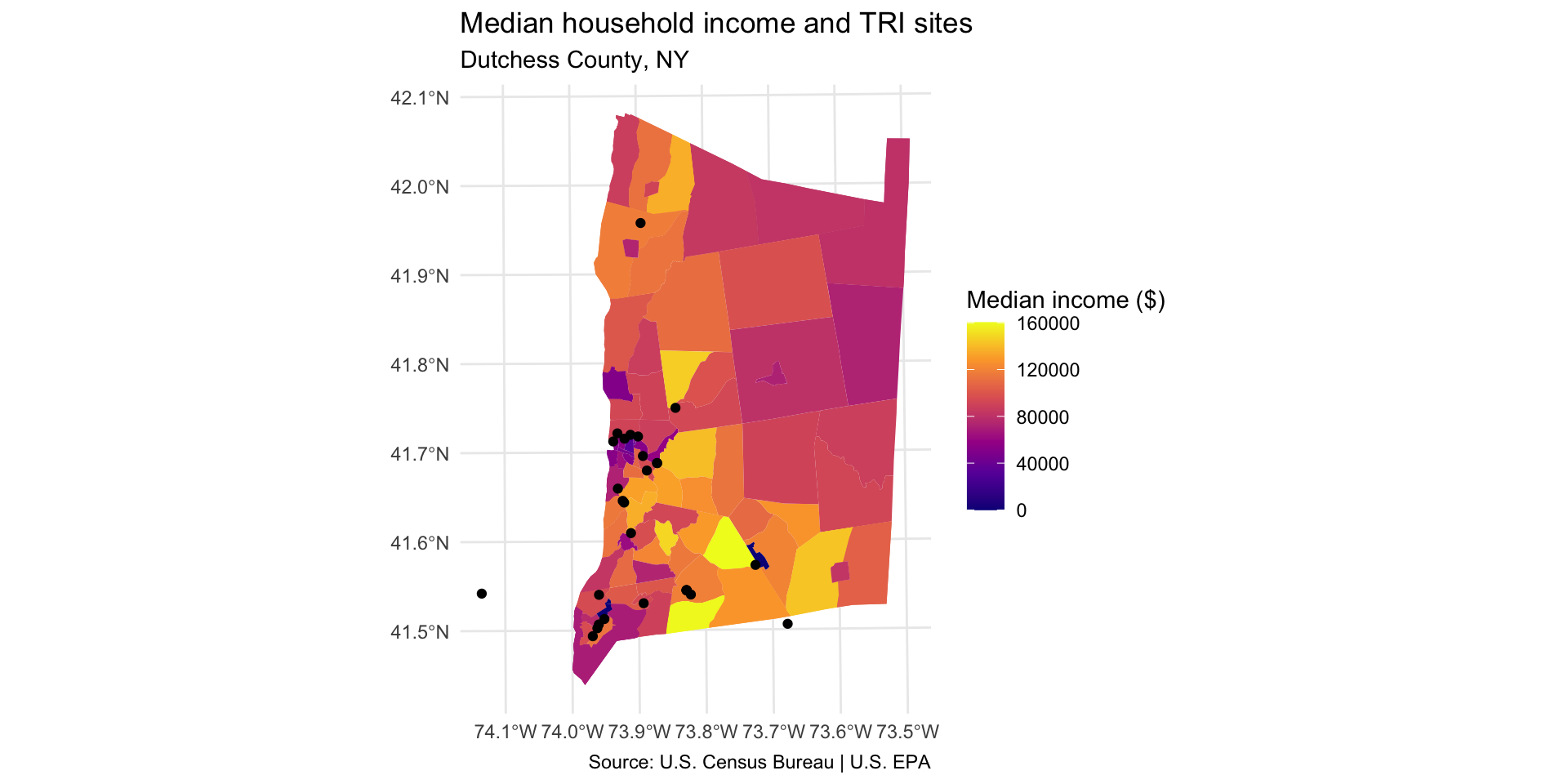

Add legend item for TRI facility points

  • Add the following to generate a legend item for the point layer:

    • aes(color = "TRI facilities") mapping function generates a legend item

    • Set color aesthetic in scale_color_manual()

dutchess_tri %>%
  ggplot() +
  geom_sf(aes(fill = median_hh_income), color = NA) +
  scale_fill_viridis_c(option="C", name="Median income ($)") +
  geom_sf(
    data = tri_dutchess,
    aes(color = "TRI facilities"), # mapped aesthetic makes legend item appear
    size = 1.5
  ) +
  scale_color_manual(
    name = NULL,  # no legend title
    values = c("TRI facilities" = "#252525")
  ) +
  labs(title="Median household income and TRI sites", 
       subtitle="Dutchess County, NY",
       caption = "Source: U.S. Census Bureau | U.S. EPA"
       ) +
  theme_minimal()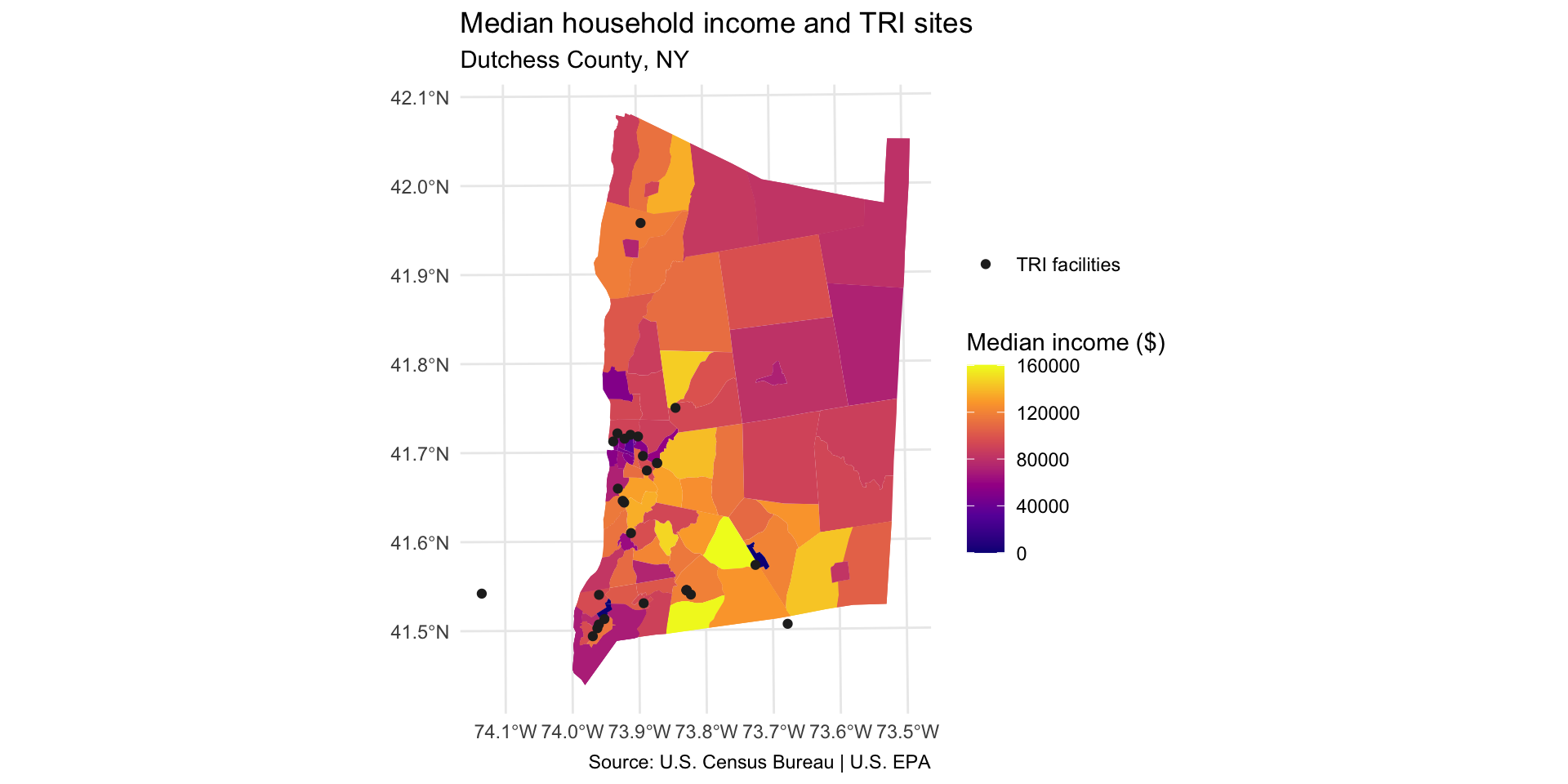

Discussion

  1. Identify and describe which parts of the county have higher TRI density. Use cardinal directions (north, south, east, west).

  2. Describe one pattern in terms of: income, asthma, or an indicator you choose.

  3. Why do you think we observe these relationships? Come up with one hypothesis that explains the pattern you observe.

Share with the class

  • What pattern did you see?

  • What might explain it?