Exploratory data analysis and visualization

Intro to Data Analytics

Why we visualize data

Explore data
Tell stories, discursive and argumentative communication

Chart responsibly

Storytelling with data comes with responsibility.
It’s easy to manipulate perception through design choices.
Consider crime maps in major cities: If only raw crime numbers are displayed, high-population areas will always appear as the most dangerous. However, normalizing by population density or comparing trends over time provides a more accurate story.

Questions to ask

Every visualization carries an implicit argument, whether we acknowledge it or not. Ask:

What am I emphasizing? What am I leaving out? What assumptions am I making about my audience?

Great visualizations don’t just present data—they invite dialogue.

Notes on where we are heading

More dplyr and ggplot basics. Learning outcomes:
- Know how to summarize data in tables and plots.
- Know how to use categorical and numerical data in plots.
Then, moving on to data wrangling: reshaping data (Ch 11) and table joins (Ch 12)
Then more visualization and statistical analysis

Why are we here?

Exploratory Data Analysis!

Exploratory Data Analysis

“A state of mind”

Generate questions about your data.
Search for answers by visualizing, transforming, and modelling your data.
Use what you learn to refine your questions and/or generate new questions.

Exploratory Data Analysis refers to the critical process of performing initial investigations on data so as to discover patterns,to spot anomalies,to test hypothesis and to check assumptions with the help of summary statistics and graphical representations.

Learn more: What is EDA?

Exploratory Data Analysis

What type of variation occurs within my variables?
What type of covariation occurs between my variables?

Exploratory Data Analysis

Summarizing data
- Summary statistics
- Univariate plots (geom_line, distribution plots)
- Bar plots
Understanding relationships between variables
- Scatter plots
Understanding and comparing distributions
- Side-by-side box plots or violin plots

What are the geoms we have used so far?

Some review: ggplot

Basic components

Data – data frame object
Geometry – geom_* can have more than one on a plot
Aesthetic mapping – aes() connects data properties and graph features – what must go in there and what can go in there depends on the geometry being used.

Basic visualizations

Histogram: distribution across buckets
Smooth density plot: the proportion of observations, “pretty histogram”
Bar chart: distribution of observations across categories

Basic visualizations

Histogram: numeric data, across a range of values on the x-axis.
Smooth density plot: numeric data, x-axis is numbers, y-axis is proportion of the whole
- A density plot is a smooth curve that shows the proportion of data in each range. The height of the curve indicates the proportion of data in that range, not how many times a value appears
Bar chart: categorical data, the x-axis is categories

Distribution plots

Univariate summaries

Summarizing the distribution of a variable

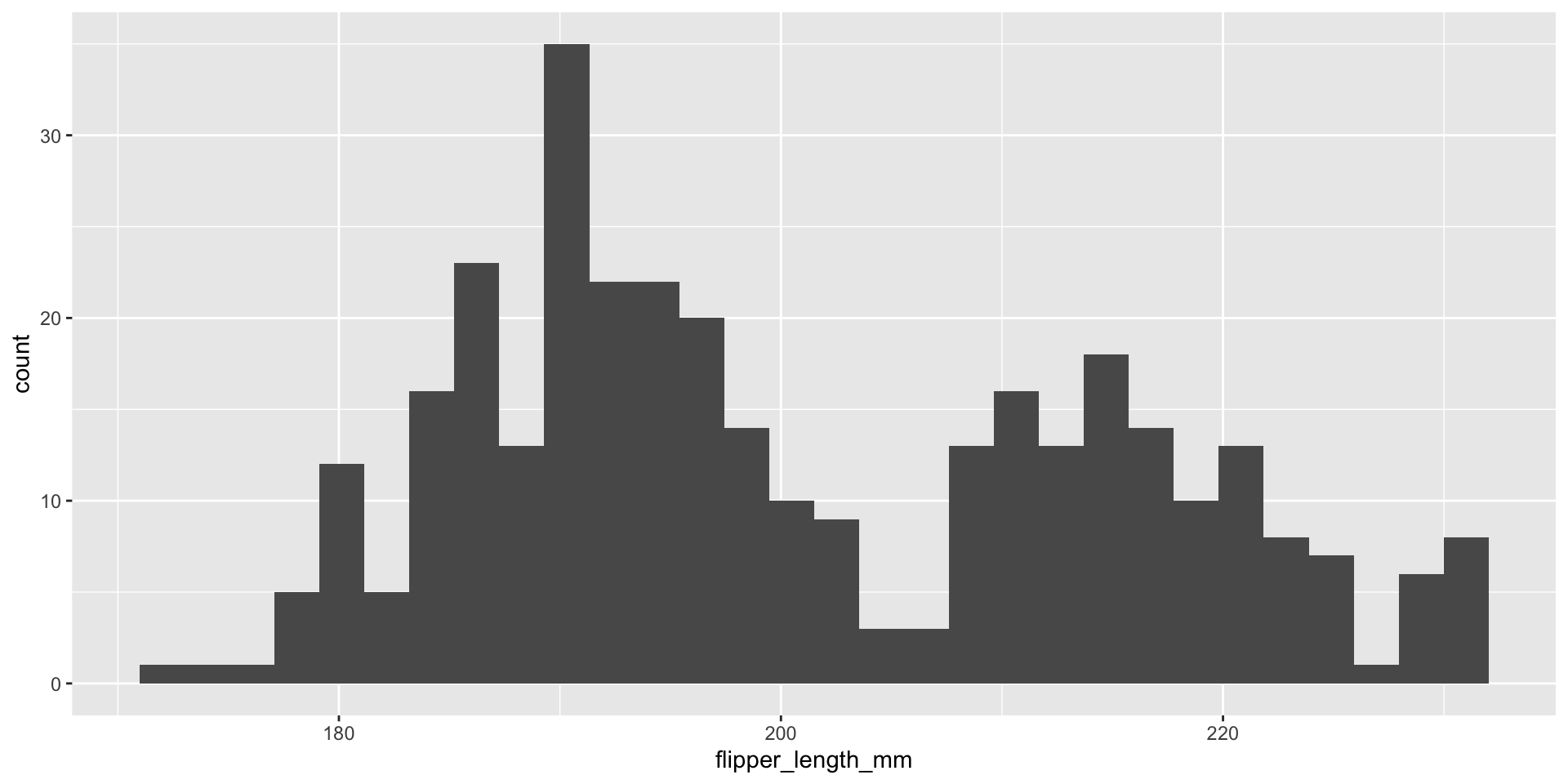
Do the lengths of flippers vary across different species of penguins? Let’s first try to understand the distribution penguin flipper length.

First, let’s load a new package palmerpenguins:

#Install and load the palmerpenguins package
#install.packages(palmerpenguins)
library(palmerpenguins)

Histogram plot

ggplot(
  data = penguins,
  mapping = aes(x = flipper_length_mm) # the x coordinate (aesthetic) is mapped to the flipper_length_mm 
) + 
  geom_histogram()

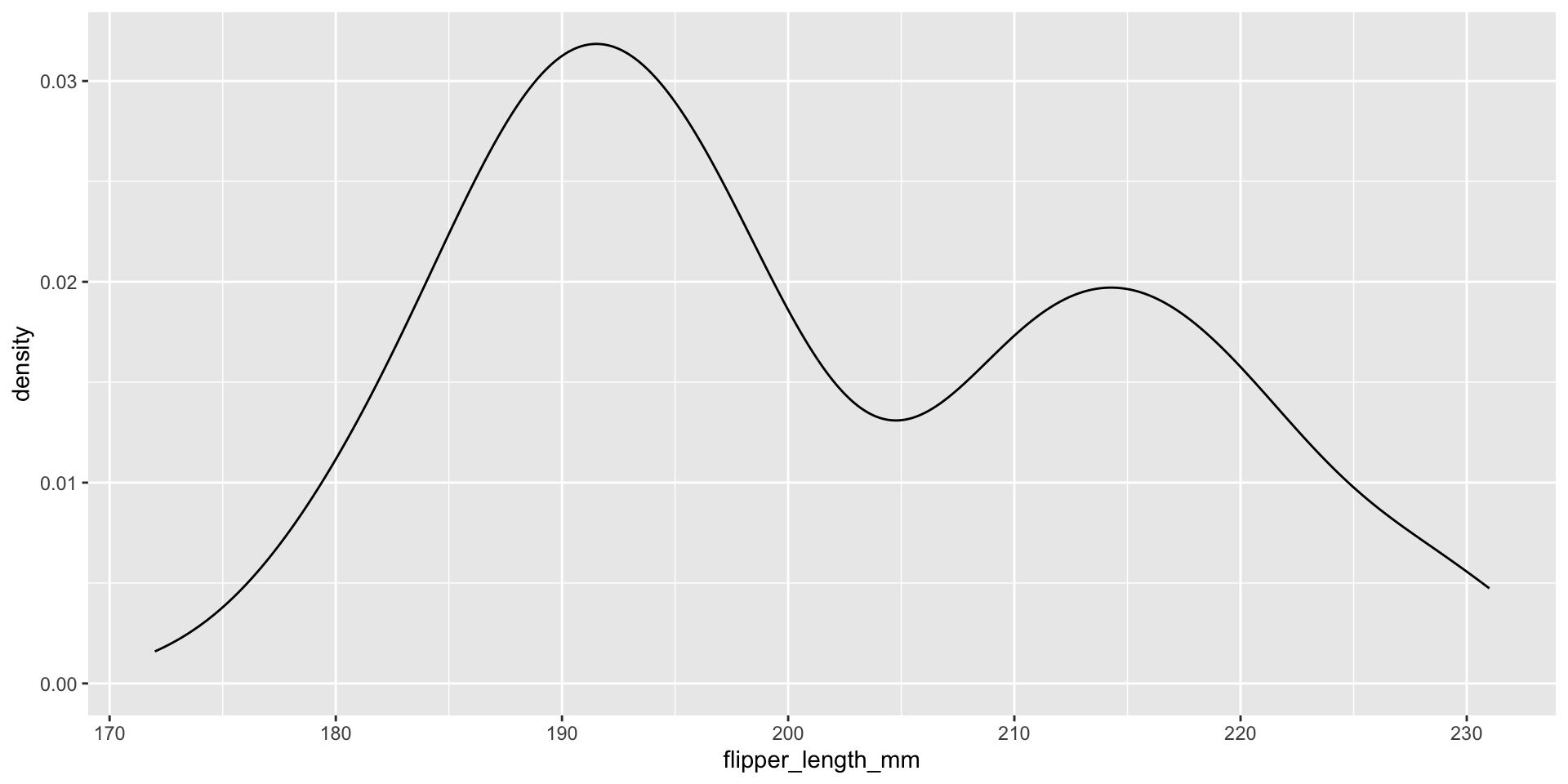
Density plot

ggplot(
  data = penguins,
  mapping = aes(x = flipper_length_mm) # the x coordinate (aesthetic) is mapped to the flipper_length_mm 
) + 
  geom_density()

Smooth density plot: numeric data, x-axis is numbers, y-axis is proportion of the whole.

A density plot is a smooth curve that shows the proportion of data in each range. The height of the curve indicates the proportion of data in that range, not how many times a value appears.

Basic summary statistics

mean
median
mode
min
max
standard deviation

Summary statistics

Mean = average of the values, central tendency measure
Median = middle value of the set, central tendency measure
Standard deviation = Spread or variability in numerical variable

Distribution plots

Sometimes the median and mean aren’t enough to understand a data set. Are most of the values clustered around the median? Or are they clustered around the minimum and the maximum with nothing in the middle? When you have questions like these, distribution plots are your friends.

The most basic statistical summary of a list of objects or numbers is its distribution.

Learn more: https://flowingdata.com/2012/05/15/how-to-visualize-and-compare-distributions/

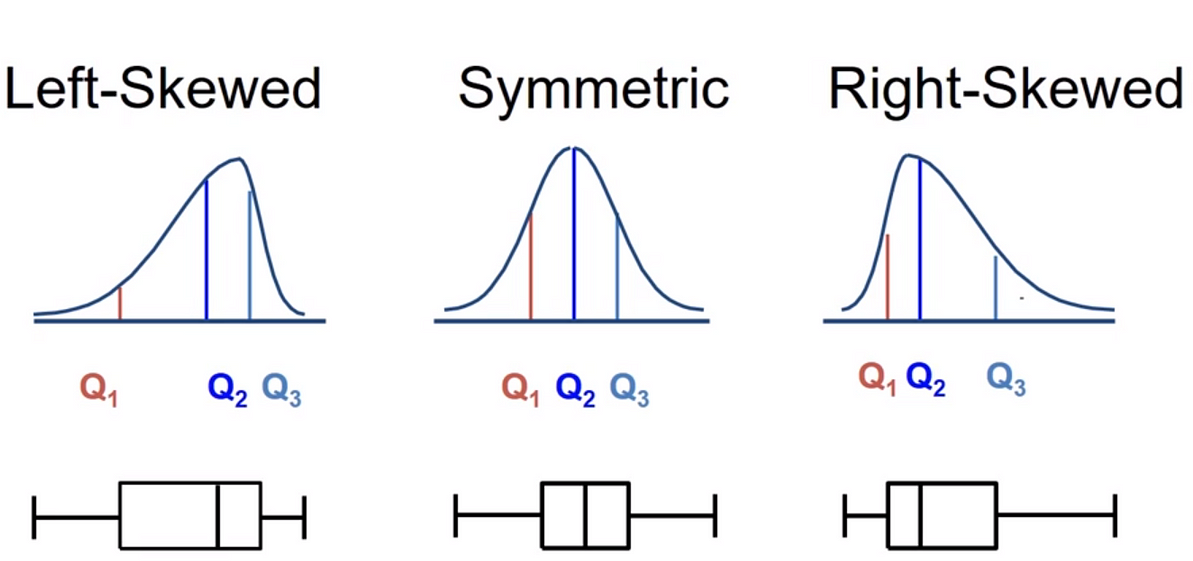
Describing shapes of numerical distributions

shape:
- skewness:
  - right-skewed,
  - left-skewed,
  - symmetric
- modality (how many peaks or modes a data distribution has): unimodal, bimodal, multimodal, uniform
center: mean (mean), median (median), mode (not always useful)
spread: range (range), standard deviation (sd), inter-quartile range (IQR)
unusual observations

Describing shapes of numerical distributions

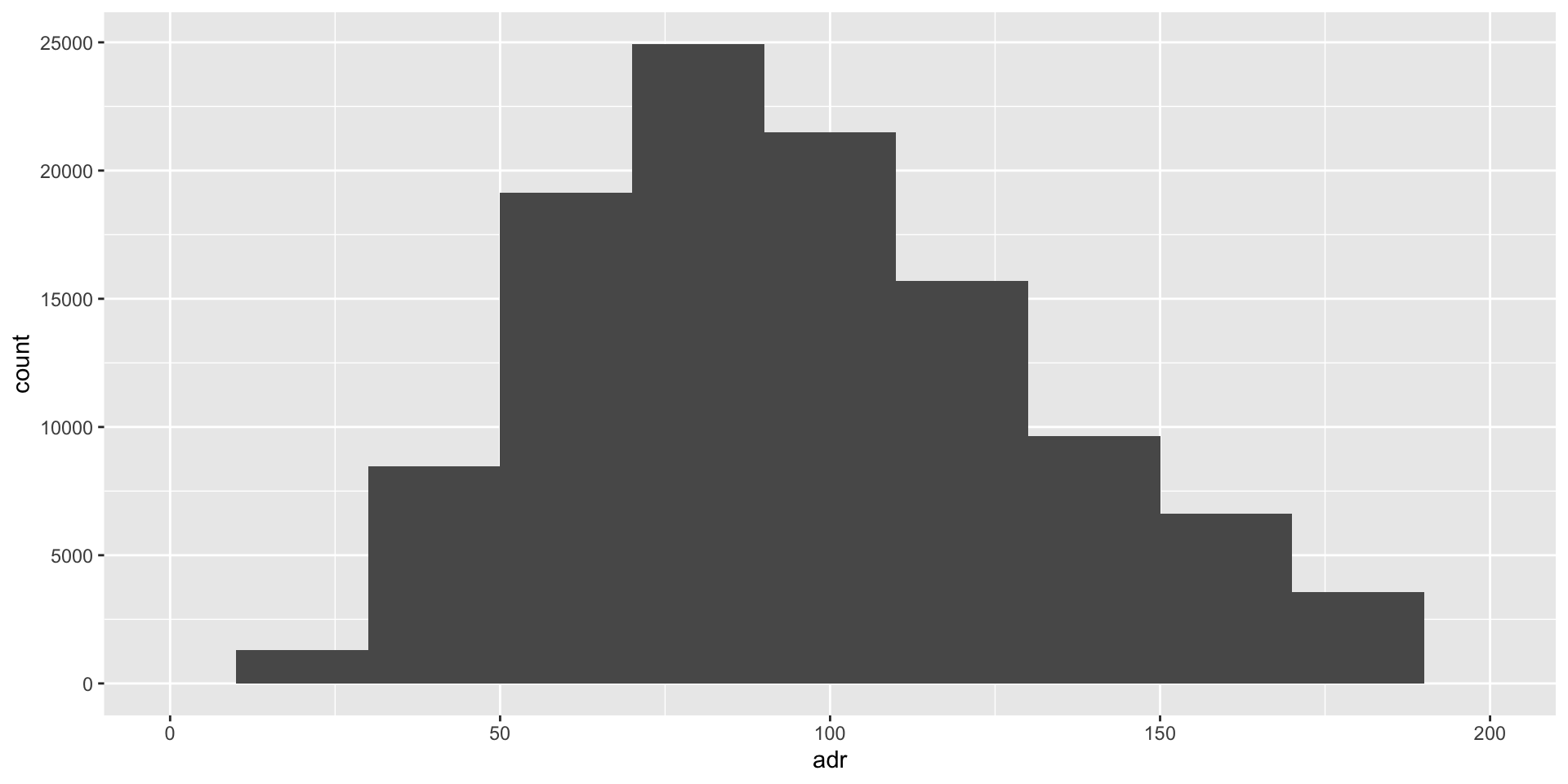
Hotels

Load the hotels data

hotels <- read_csv("data/hotels.csv")

Calculating summary statistics

What is the mean & standard deviation for hotels$adr?

hotels %>% 
  summarize(average = mean(lead_time), 
            standard_deviation = sd(lead_time))

# A tibble: 1 × 2
  average standard_deviation
    <dbl>              <dbl>
1    104.               107.

adr is the average daily rate for a hotel booking

Hotels

ggplot(hotels, aes(x = adr)) +
  geom_histogram(binwidth = 20) +
  xlim(0,200)

Hotels

ggplot(hotels, aes(x = adr)) +
  geom_density(fill = "blue") +
  xlim(0,200)

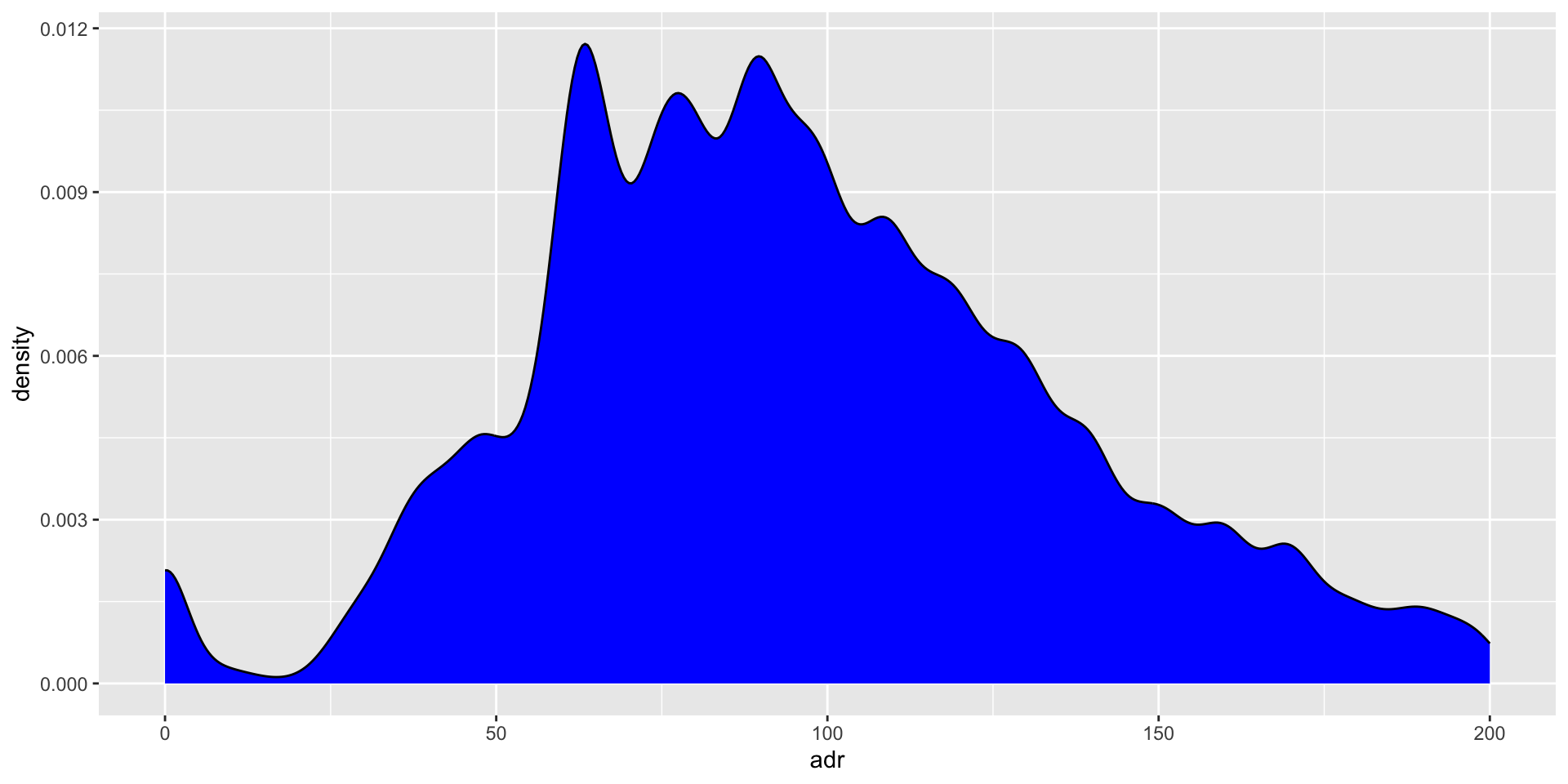
Hotels

Add a marker at the mean with geom_vline

ggplot(hotels, aes(x = adr)) +
  geom_density(fill = "blue") +
  xlim(0,200) + 
  geom_vline(aes(xintercept=mean(adr)),
            color="black", linetype="dashed", size=1)

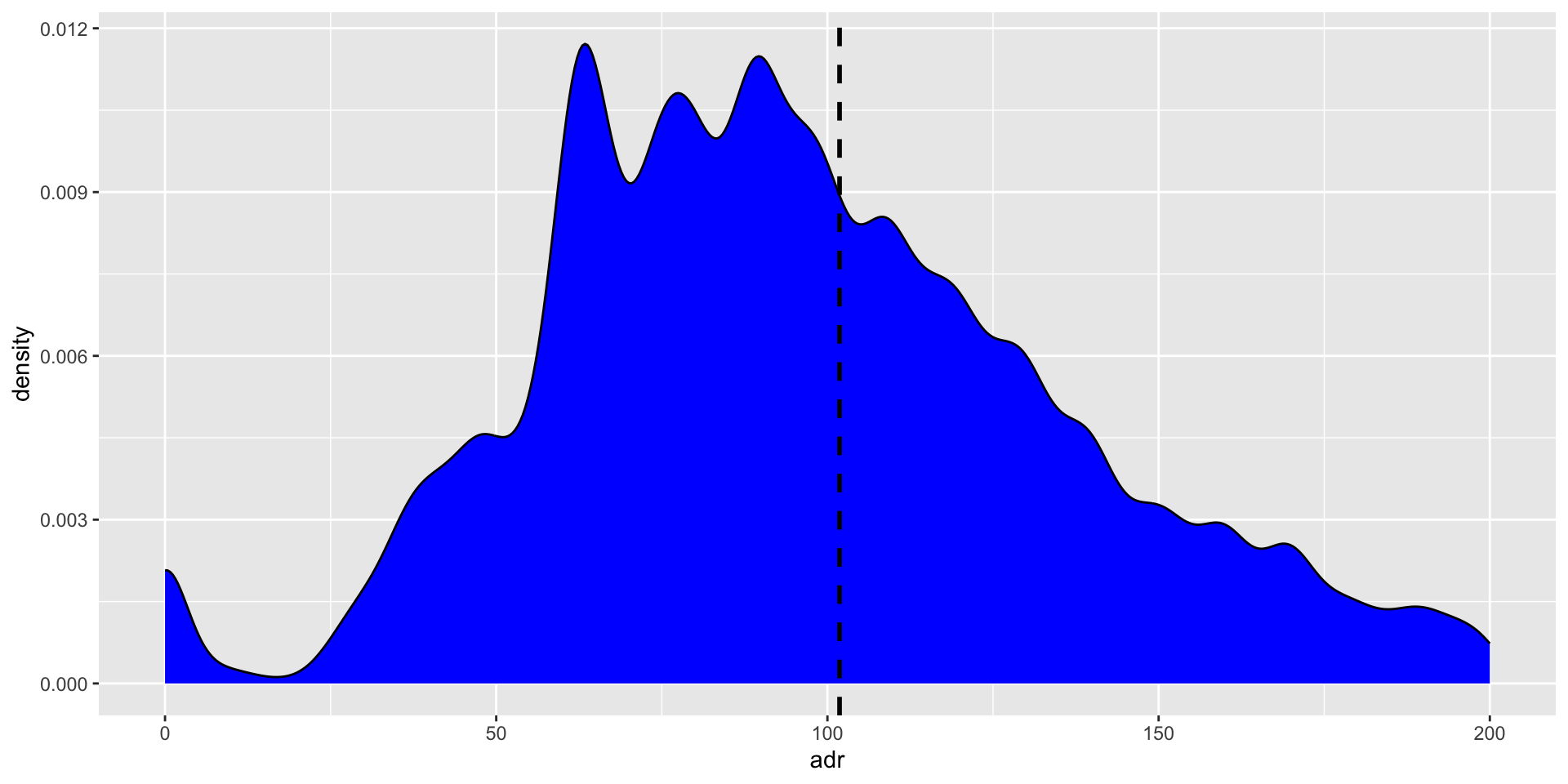
Hotels

Add a marker at the mean

ggplot(hotels, aes(x = adr)) +
  geom_density(fill = "blue") +
  xlim(0,200) + 
  geom_vline(aes(xintercept=mean(adr)),
            color="black", linetype="dashed", size=1)

The mean is the most frequently used measure of central tendency because it uses all values in the data set to give you an average.

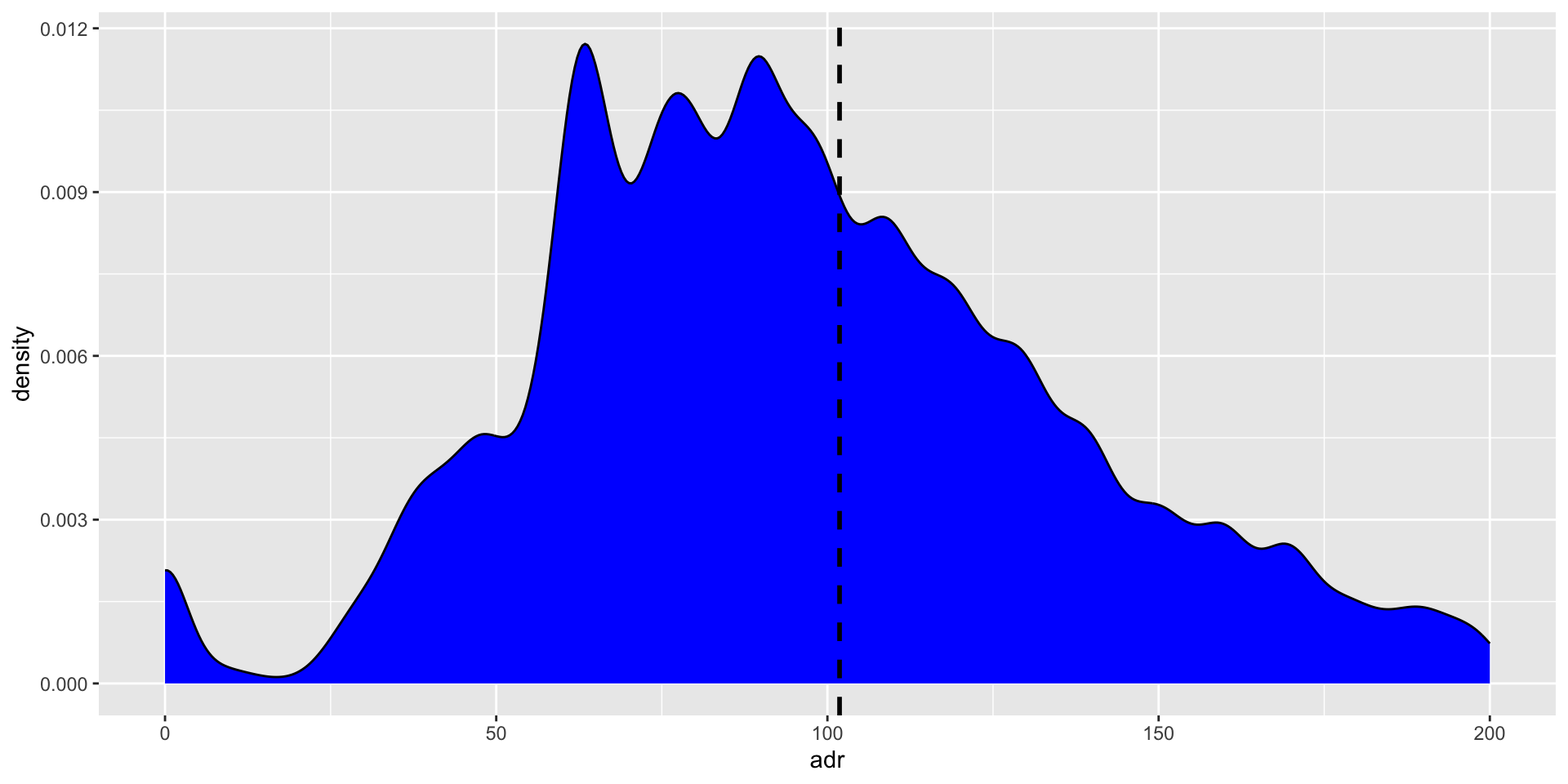
Try adding a marker at the median

Central tendency

For data from skewed distributions, the median is better than the mean because it isn’t influenced by extremely large values.

Learn more (link)

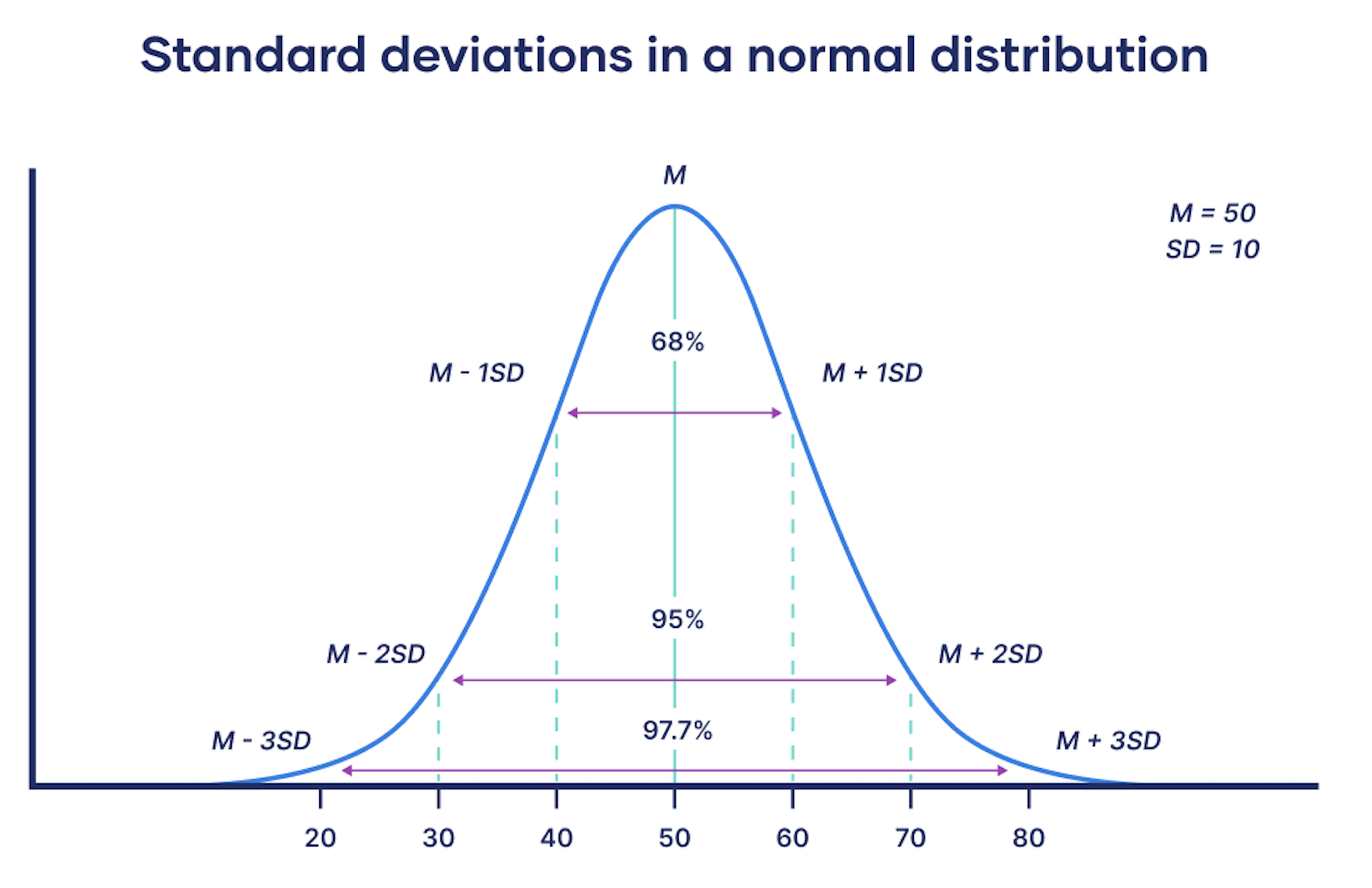
Standard deviation

For each value in the data set, we compute its deviation from the mean

\[ x_i - \bar{x} \]This will generate some negative and some positive values, so to get them to be positive we square them.

Then, add these up to compute the average deviation, or sample variance:

\[s^{2}= ∑(x_i−\bar{x})^2 / n-1\]

Take the square root to get the standard deviation: \[s\]

Calculating standard deviation

Let’s try this out in R

test <- data.frame(nums = seq(1, 50, 3))

test %>% 
  summarize(avg = mean(nums),sdev = sd(nums))

test2 <- data.frame(nums = c(24,24,24,24,24,24,24,24,25,26,26,26,26,26,26,26,26))

test2 %>% 
  summarize(avg = mean(nums),sdev = sd(nums))

Standard deviation

test <- data.frame(nums = seq(1, 50, 3))

test %>% 
  summarize(avg = mean(nums),sdev = sd(nums))

  avg     sdev
1  25 15.14926

test2 <- data.frame(nums = c(24,24,24,24,24,24,24,24,25,26,26,26,26,26,26,26,26))

test2 %>% 
  summarize(avg = mean(nums),sdev = sd(nums))

  avg sdev
1  25    1

Standard deviation

Calculate step-by-step

calc_standard_deviation <- test %>% 
  mutate(deviation_from_mean = nums - mean(nums),
         deviation_squared = deviation_from_mean^2) %>% 
  summarize(sum_deviation_squared = sum(deviation_squared),
            s2 = sum_deviation_squared/(17-1), # See formula for s-squared on previous slide
            sd = sqrt(s2))
calc_standard_deviation

  sum_deviation_squared    s2       sd
1                  3672 229.5 15.14926